Sistemas computacionais suportam tamanhos específicos de números, ou melhor, valores. Campos de um determinado programa que recebem ou apenas exibem valores devem possuir certos limites. Imaginemos se as calculadoras, como aquelas de bolso que se tornaram mais difíceis de encontrar a venda nos dias atuais ou as disponibilizadas em sistemas operacionais como Linux, Android, Windows ou Mac, aceitassem que usuários inserissem números do jeito que bem entendessem. Isso provavelmente ocasionaria erros na hora da execução dos cálculos, pois o hardware (na ocasião, microprocessadores) possuem uma quantidade fixa de bits. Deve haver uma padronização entre o que é digitado e o que é levado para o cálculo propriamente dito.

Valores inferiores, tanto na entrada quanto na exibição, apresentam erros chamados de underflow. Valores superiores (entrada ou exibição), apresentam erros chamados overflow. Pensando em evitar ou tratar quaisquer tipos de erros, existe o sistema de ponto (ou vírgula) flutuante. Este sistema é representado pela fórmula F[β, t, -p, p]. O “F” representa o sistema, o β a base, enquanto que “t” representa a quantidade de número na mantissa (números após a vírgula), “-p” para limite mínimo do expoente e “p” para limite máximo de expoente.

Digamos, por exemplo, que seja necessário representar o sistema F[2, 2, -3, 3]. Da fórmula mostrada anteriormente, o valor “2” substitui “β”, “2” substitui “t”, “-p” substitui “-3” e “p” substitui “3”. Ou seja, o menor valor aceito pelo sistema é “0,0625” e o maior, “6”. Números inseridos ou resultados de cálculos inferiores a “0,0625”, ocorre underflow. Números inseridos ou resultados de cálculos superiores a “6”, ocorre overflow. Entendo que pode ter ficado confuso, mas a explicação prática ocorre nas próximas linhas.

Antes de entrarmos em explicações com exemplos, é importante entender a diferença entre arredondamento e truncamento de números. Dado o valor aleatório “1,38712284857485569”, temos que deixá-lo com apenas 6 números após a vírgula. Para o caso de um arredondamento, o número será escrito da seguinte forma: “1,387123”. Ou seja, como o sétimo número é maior que 5, o seu antecessor recebe o incremento de 1 e ocorre o arredondamento e eliminação dos demais. Já para o caso de truncamento, apenas são cortados os demais números após a sexta casa, ficando “1,387122”. Irão perceber que nos exemplos utilizados no decorrer do artigo, foi utilizado apenas o truncamento.

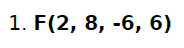
Conforme acima, foi dado um sistema com base 2, com 8 dígitos na mantissa, até -6 de expoente mínimo e até 6 de expoente máximo.

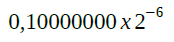
A regra diz que para o valor mínimo a primeira casa após a vírgula deve ser diferente de 0. No caso, foi colocado 1. Segue sendo multiplicado por 2 elevado a sexta negativa.

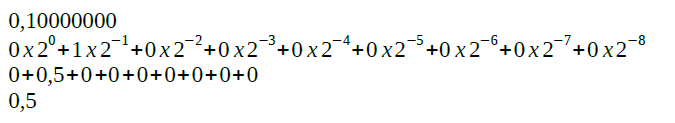
Em seguida transformamos “0,10000000” que está na base binária em decimal (é muito mais fácil calcular).

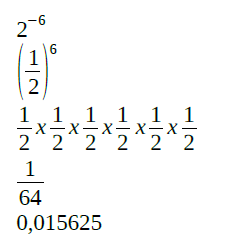
Aqui também é necessário calcular, para que na sequência ocorra a multiplicação.

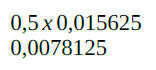
Então chegamos ao valor 0,5 (vindo de 0,10000000) sendo multiplicado por 0,015625 (vindo de 2 elevado à sexta). Esta operação resulta no valor “0,0078125”. Ou seja, este é o valor mínimo aceito pelo sistema.

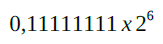
Para continuar com o cálculo, a mantissa acima foi completada com o maior dígito do sistema binário: 1.

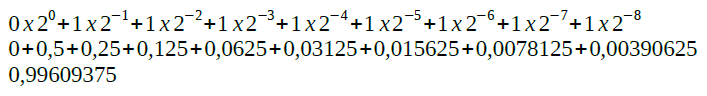
Em seguida transformamos “0,11111111” que está na base binária em decimal (é muito mais fácil calcular).

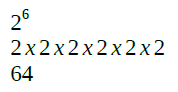
Aqui também é necessário calcular (resolver a exponenciação), para que na sequência ocorra a multiplicação.

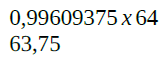
Então chegamos ao valor 0,99609375 (vindo de 0,11111111) sendo multiplicado por 64 (vindo de 2 elevado à sexta). Esta operação resulta no valor “63,75”. Ou seja, este é o valor máximo aceito pelo sistema. Ou seja, o sistema F[2, 8, -6, 6] trabalha com valores de 0,0078125 a 63,75. Qualquer coisa abaixo ou acima, respectivamente, são considerados underflow e overflow.

Agora sim, vamos aos testes. Vamos tentar resolver contas aleatórias. Algumas podem dar overflow, outras podem dar underflow. Tanto na entrada, quanto na apresentação do resultado. Outras não apresentarão erro e com estas poderemos seguir com os cálculos.

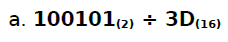
A primeira conta a ser feita é 100101 na forma binária, dividido por 3D na forma hexadecimal. Observem os valores 2 e 16 subscritos.

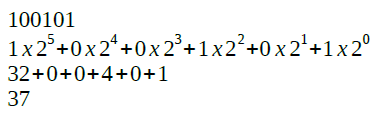
Primeiramente convertemos o valor binário para decimal.

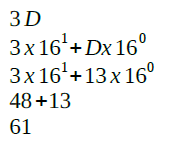
Na sequência também convertemos o valor hexadecimal para decimal.

Chegamos a dois valores. O primeiro representa o valor exato (0,6065573770491803) e o segundo representa o valor que cabe na mantissa de 8 (0,60655737), conforme anteriormente determinado. Observem que ele foi simplesmente cortado após a oitava casa depois da vírgula.

A fórmula acima se dá para que seja calculado o erro absoluto. Também foram deixados como resultados os valores com e sem notação científica.

Acima foi calculado o erro relativo. Os valores também foram deixados com e sem notação científica. Observe que o erro relativo é geralmente expresso em porcentagem.

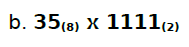
Uma nova conta a ser feita é 35 na forma octal multiplicado por 1111 na forma binária.

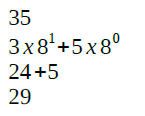
Convertendo o 35 octal para decimal para facilitar os cálculos. Observem que o valor (29) está entre o mínimo (0,0078125) e máximo (63,75) permitido pelo sistema. Logo, sem erros até então.

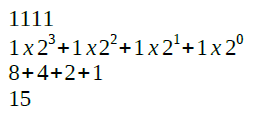
Convertendo o 1111 binário para decimal para facilitar os cálculos. Observem que o valor (15) está entre o mínimo (0,0078125) e máximo (63,75) permitido pelo sistema. Logo, sem erros até então.

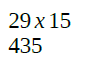
Agora sim, após ambos os valores (octal e binário) convertidos, consigo fazer a conta com mais facilidade. Reparem que o valor do resultado (435) foi superior ao permitido pelo sistema (63,75); neste caso ocorreu um erro overflow. A conta termina aqui.

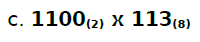
Vamos a mais uma conta, para o mesmo sistema. Desta vez temos 1100 na forma binário sendo multiplicado por 113 na forma octal.

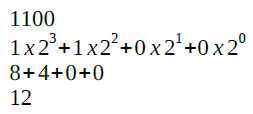
Primeiro, convertemos o valor binário para decimal. O valor (12) está entre o mínimo (0,0078125) e máximo (63,75) permitido pelo sistema. Logo, sem erros até então.

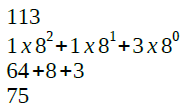
Para continuar, vamos converter o valor 113 também para decimal. Observe que chegamos a um resultado de 75 e este valor é superior ao permitido pelo sistema (63,75); neste caso ocorreu um erro overflow e conta termina aqui.

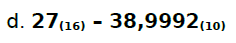
Uma nova conta. Aqui está pedido para subtrair 38,9992 na base decimal de 27 na base hexadecimal.

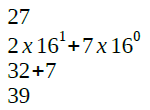
Primeiramente convertemos o valor 27 hexadecimal para decimal. O valor (39) está entre o mínimo (0,0078125) e máximo (63,75) permitido pelo sistema. Logo, sem erros até então.

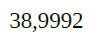
O valor 38,9992 já está em decimal, o que dispensa conversões.

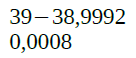
O resultado da conta resulta em 0,0008. Ou seja, o obtido é menor que o permitido pelo sistema (0,0078125). Isso resulta em underflow e a conta termina aqui.

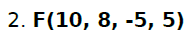
Aqui temos um novo sistema. Observem que este agora está na base decimal (10), diferente do sistema anterior que era binário (2). Este sistema também pede 8 dígitos na mantissa. Já os expoentes máximo (positivo) e mínimo (negativo) são 5.

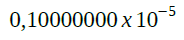
A regra diz que para o valor mínimo a primeira casa após a vírgula deve ser diferente de 0. No caso, foi colocado 1. Segue sendo multiplicado por 10 (agora o sistema é decimal), elevado a quinta negativa.

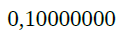
Aqui não há conversão visto que o valor (0,10000000) já está em decimal.

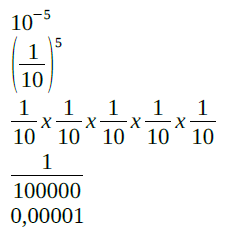
Vamos transformar o valor 10 elevado à quinta negativa em um número com ponto flutuante para facilitar os cálculos. Dez elevado a quinta negativa é a mesma coisa que um sobre dez elevado a quinta positiva.

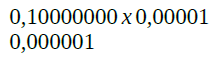
Agora sim, multiplicando o valor 0,10000000 por 0,00001 (vindo de dez elevado a quinta negativa), chegamos ao valor mínimo do sistema (0,000001).

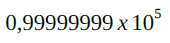
Para continuar com o cálculo, a mantissa acima foi completada com o maior dígito do sistema decimal: 9.

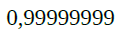
Aqui não há conversão visto que o valor (0,99999999) já está em decimal.

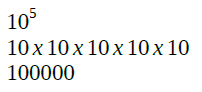
Aqui também é necessário calcular (resolver a exponenciação), para que na sequência ocorra a multiplicação.

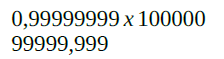
Então chegamos ao valor 0,99999999 sendo multiplicado por 100000 (vindo de 10 elevado à quinta). Esta operação resulta no valor “99999,999”. Ou seja, este é o valor máximo aceito pelo sistema.

Para as próximas contas (a e b) temos 1290 na base hexadecimal sendo dividido por 27 na base octal. Este cálculo não ocorre overflow nem underflow e é posível saber tanto o erro absoluto, quanto o erro relativo. Já o cálculo 201,1432 na base octal sendo multiplicado por 190FF na base hexadecimal, temos com resultado 102655 decimal. O valor é maior que o sistema permite e portanto ocorre erro de overflow.

Fiquem com os cálculos:

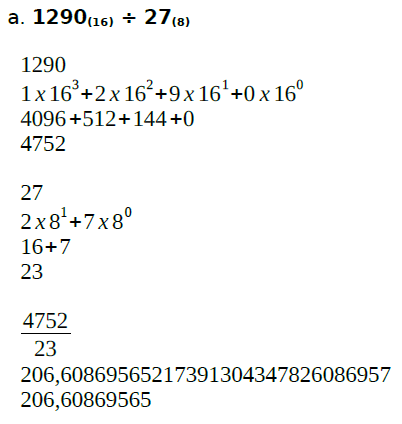
Esta foi uma prévia do Sistema de Ponto Flutuante. Foram demonstrados 2 sistemas: um de base binária (2) e com 4 contas feitas (a, b, c e d) e outro com base decimal (10) e com 2 contas feitas (a e b).

Como puderam perceber este sistema é um pouco complexo, porém com alguns minutos de estudo, vão conseguir de fato entender o processo. Espero que de alguma forma eu possa ter contribuído para seu aprendizado.